Subtrajectory Clustering
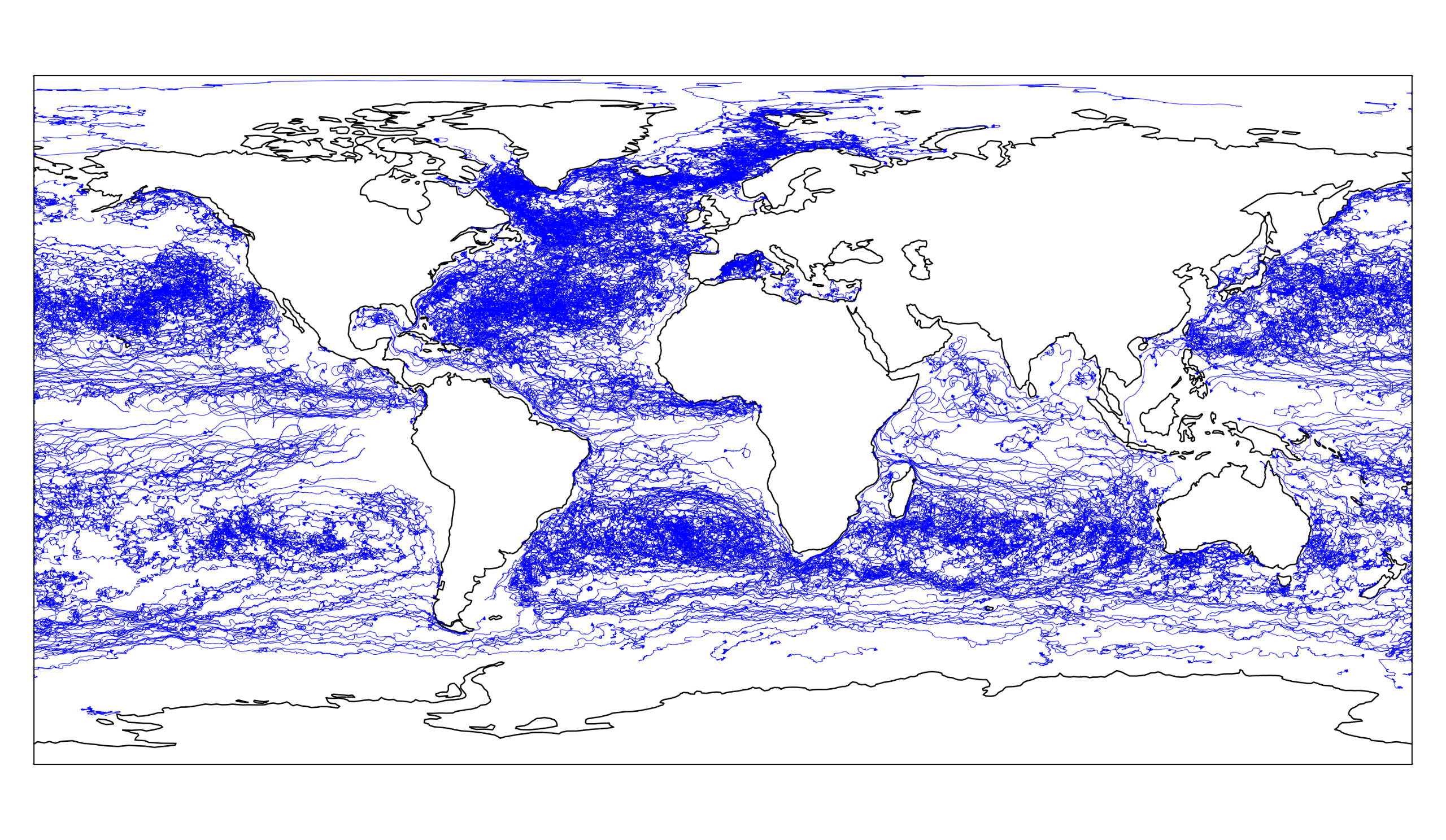
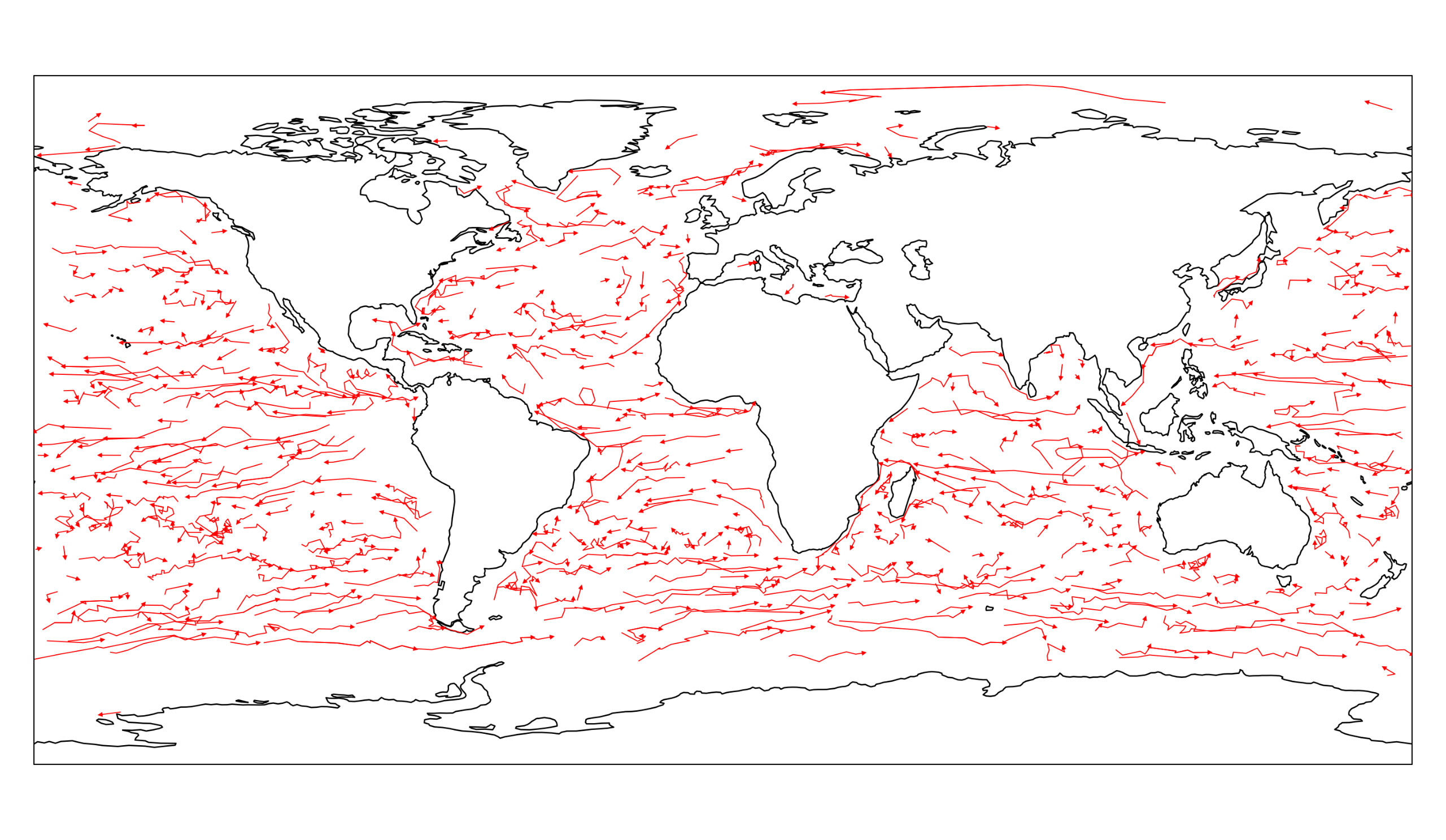
Clustering movement data, such as GPS trajectories, is a central challenge in spatio-temporal analysis. Our research addresses this challenge through a geometric set cover problem. The goal: Given a polygonal curve with complexity $n$, find the smallest number $k$ of representative trajectories (each with complexity at most $\ell$). Every point on the input trajectory must lie on a subtrajectory that stays within Fréchet distance $\Delta$ of a representative curve.
2022: Reducing to Geometric Set Cover
In 2022, Frederik Brüning, Anne Driemel, and I tackled this problem by reducing it to a classical geometric set cover instance. We focused on representative curves that are line segments. Our approach applied geometric set cover techniques, including a variation of the multiplicative weights update method introduced by Brönniman and Goodrich for low VC-dimension cases.
We developed a bicriteria-approximation algorithm. It computes $O(k \log k)$ line segments that cover a polygonal curve with $n$ vertices under Fréchet distance $\leq 11\Delta$. The algorithm runs in expected time $\tilde{O}(k^2n + kn^3)$ and uses $\tilde{O}(kn + n^3)$ space. For $c$-packed input curves, the expected time is $\tilde{O}(k^2c^2n)$, and space usage is $\tilde{O}(kn + c^2n)$.
2023: Extending to Non-Constant Complexity Curves
In 2023, Anne Driemel and I extended our method to allow representative curves with non-constant complexity. We aimed to build a practical proof-of-concept implementation. Our new approach computes curves of size $O(k \log n)$ in time $\tilde{O}(\ell^2 n^4 + k \ell n^4)$, while maintaining the same distance guarantee of $11\Delta$. Each curve can include sub-curves of complexity up to $\ell$. We tested our algorithm on ocean current tracking data and full-body motion data. The results showed that our method is effective for analyzing large spatio-temporal datasets.2025: Subcubic Approximation Algorithm
In 2025, Anne Driemel and I improved the algorithm’s theoretical performance. We were motivated by recent work from Ivor van der Hoog, Thijs van der Horst, and Tim Ophelders, who showed that this problem allows an algorithm with running time $\tilde{O}(k n^3)$. We present the first deterministic subcubic-time approximation algorithm for this problem. It runs in $O((n^2 \ell + \sqrt{k} n^{5/2}) \log^2 n)$. This algorithm achieves a bicriteria approximation: It relaxes the Fréchet threshold by a factor of 4 and the solution size by $O(\log n)$.Non-obtuse Triangulations
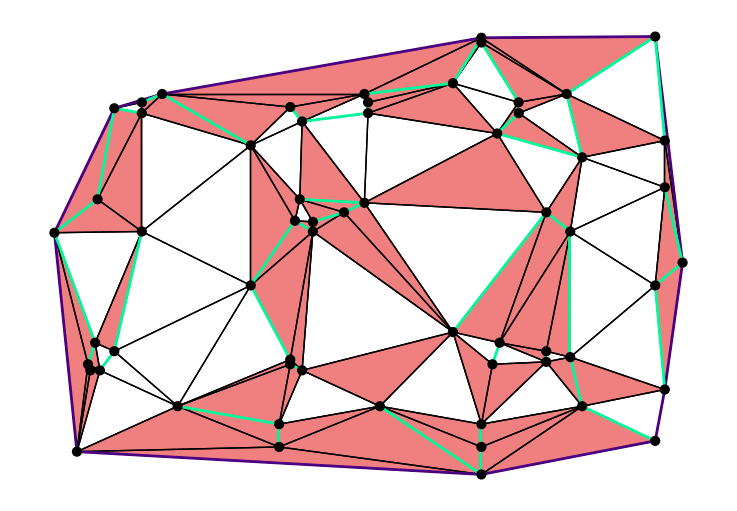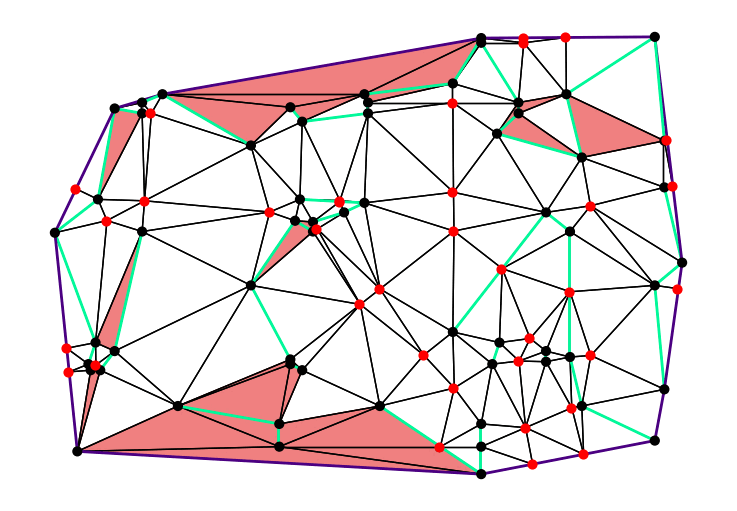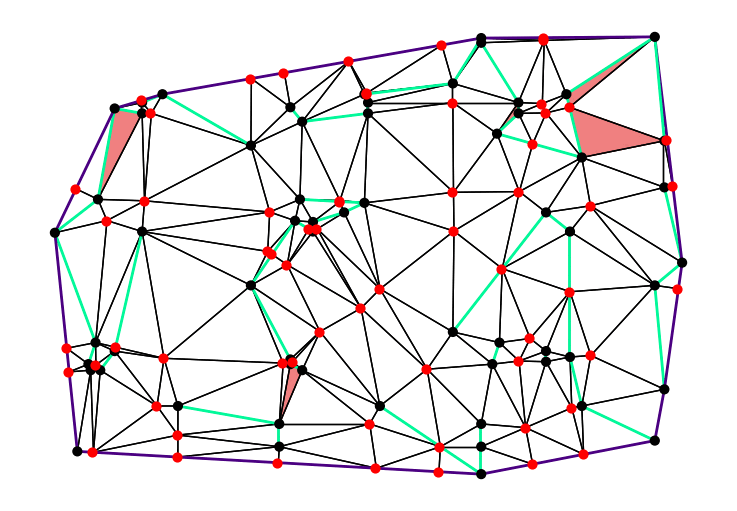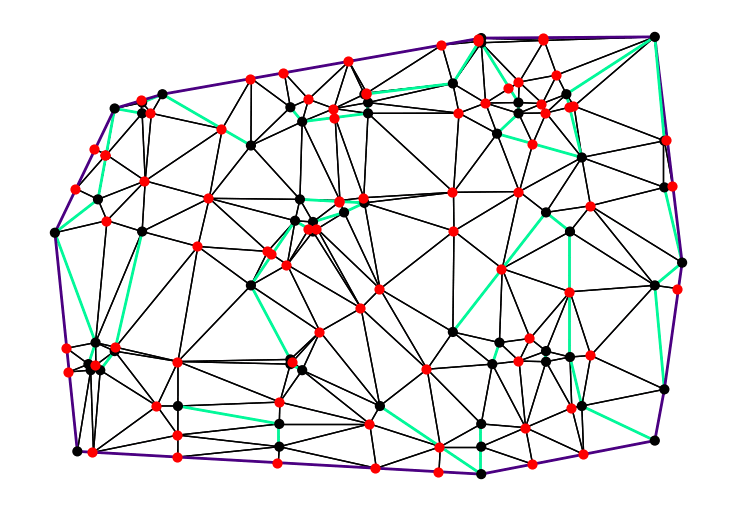
In late 2024, Mikkel Abrahamsen, Florestan Brunck, Benedikt Kolbe, André Nusser, and I joined forces for the annual CG:SHOP competition. The 2025 edition challenged participants to generate high-quality triangulations of planar straight-line graphs. Each triangle had to be non-obtuse. To make this possible, Steiner points could be added when necessary. The main goal was to use as few Steiner points as possible. We won the competition and were invited to present our work at SoCG 2025.
Our method performs a local search across possible triangulations. We first compute a small set of candidate Steiner points. Then, the algorithm selects one of these points based on a game-tree-inspired evaluation function and adds it to the triangulation. This process repeats until no obtuse triangles remain. For the given instances, our solution used fewer Steiner points than the number of input vertices $n$. This is a significant improvement over the best-known theoretical upper bound of $O(n^{5/2})$, proven by Christopher Bishop.
Fréchet Distance Variants
The Fréchet distance is a widely used measure for comparing polygonal curves. However, it is sensitive to outliers and assumes that inputs are polygonal or noisy in a specific way. These limitations reduce its robustness in real-world applications.
2022: A Variant of the Fréchet Distance to Handle Outliers
In 2022, Anne Driemel and I developed a variant of the Fréchet distance designed to address outliers. The problem is defined as follows: Given two polygonal curves $T$ and $B$, each with at most $n$ vertices, a parameter $k$, and a threshold $\delta$, can we insert $k$ shortcuts along $B$ so that its Fréchet distance to $T$ is at most $\delta$?
We analyzed this problem for polygonal curves in the plane and proved several results:
- We gave a decision algorithm with running time $O(k n^{2k+2} \log n)$.
- Assuming the Exponential-Time Hypothesis (ETH), no algorithm can solve the problem in time $n^{o(k)}$.
Despite the hardness result, we also found efficient approximation strategies. We proposed a $(3 + \varepsilon)$-approximate decider that runs in $O(k n^2 \log^2 n)$ time for fixed $\varepsilon$. If $k$ is constant and the input curves are $c$-packed, the algorithm runs in near-linear time.
2024: Extending Fréchet Distance Algorithms to Algebraic Curves
In 2024, Anne Driemel, Benedikt Kolbe, and I extended efficient Fréchet distance algorithms to work with algebraic curves. We introduced a decomposition of the free space diagram into a manageable number of pieces. This allowed us to apply polygonal techniques to more general curve classes.
Given two continuous curves made up of $m$ and $n$ smooth segments (each from a well-behaved class such as algebraic curves of bounded degree), our algorithm solves the decision problem in $O(mn)$ time.
We also adapted the existing $(1 + \varepsilon)$-approximation framework for piecewise smooth, $c$-packed curves. Our method computes an approximate decision in $O(cn / \varepsilon)$ time for any $\varepsilon > 0$.
2025: Efficient Algorithm for Translation- and Scaling-Invariant Fréchet Distance
In 2025, Lotte Blank, Anne Driemel, Benedikt Kolbe, André Nusser, Marena Richter, and I developed an efficient algorithm for computing the Fréchet distance between one-dimensional curves under translation and scaling.
We first presented an algorithm for translation-invariant Fréchet distance on curves of complexity $n$ with a running time of $O(n^{8/3} \log^3 n)$. This result came from a new framework tailored for 1D curves, which also enabled a second result: an algorithm for the scaling-invariant case with the same running time.
Both algorithms improve upon the previous best bound of $\tilde{O}(n^4)$ and match the performance of the discrete version. Although the approach involves technical ideas, the core concept is simple — it reduces the continuous problem to its discrete form across multiple length scales.
All things massive data
We often face massive data sets and want to answer fundamental questions efficiently. For example, we may want to cluster the input or identify the element closest to a query. These problems arise not only for points in the Euclidean plane but also for complex spatio-temporal data. While efficient data structures exist for Euclidean data, similar solutions for spatio-temporal data remain less developed.
2023: Approximate Nearest Neighbor for Curves
In 2023, Anne Driemel, Benedikt Kolbe, and I designed a data structure that solves the approximate nearest neighbor (ANN) problem for curves. Given a query polygonal curve, it returns an input curve that approximately minimizes the distance to the query.
We focused on a subspace of curves with bounded doubling dimension and small Gromov-Hausdorff distance to the full space of curves. Using advanced techniques for doubling spaces, we built a data structure that solves the $(1 + \varepsilon)$-ANN problem for any set of parametrized polygonal curves.
The expected preprocessing time is $F(d, k, S, \varepsilon) \cdot n \log n$, and the space usage is $F(d, k, S, \varepsilon) \cdot n$. Query time is $F(d, k, S, \varepsilon) \log n + F(d, k, S, \varepsilon)^{-\log(\varepsilon)}$, where
$$F(d, k, S, \varepsilon) = O\left(2^{O(d)}k\Phi(S)\varepsilon^{-1}\right)^k,$$
and $\Phi(S)$ is the spread of the set of vertices and edges in $S$. We extended these results to $c$-packed curves and derived improved bounds for small $c$.
2023: Coresets for the $(k, \ell)$-Median Problem Under DTW
Also in 2023, Benedikt Kolbe, Ioannis Psarros, Dennis Rohde, and I developed the first coresets for the $(k, \ell)$-median problem under Dynamic Time Warping (DTW). This was previously unexplored because DTW is not a metric, making it harder to apply standard techniques.
Our approach relied on three key ingredients:
- An adapted $\varepsilon$-coreset framework based on sensitivity sampling.
- New bounds on the VC-dimension of range spaces defined by DTW balls.
- New approximation algorithms for the $k$-median problem under DTW.
We studied how to approximate DTW in ways that allow the use of existing tools while keeping the accuracy high. In particular, we showed that given $n$ curves, one can define a metric that approximates DTW and supports efficient clustering. These are the first approximations with polynomial running time that match the quality of existing methods.
Our final result is a practical algorithm for approximating $(k, \ell)$-median clustering under DTW.