About me
I’m Jacobus Conradi, a postdoctoral researcher in the Algorithms and Complexity group at the University of København, where I work with Mikkel Abrahamsen. Before coming to Denmark, I was at the University of Bonn, Germany, where I worked on computational geometry under the supervision of Anne Driemel.
My research lies in computational geometry and algorithm design. I’m interested in how geometric structure shapes what algorithms can and cannot do and in understanding the fine line between problems that are efficiently solvable and those that are inherently hard. Much of my work has revolved around comparing geometric objects such as curves or trajectories: studying similarity measures, their algorithmic complexity, and how they can be used for tasks like clustering, segmentation, and nearest-neighbor search. Over time, my interests have broadened beyond similarity measures toward a wider range of geometric and combinatorial questions. I like the interplay between theory and experiment, and I often test algorithms on real data to see how well the clean theoretical picture holds up in practice.
My Journey
In 2020, I completed my undergraduate studies in Bonn and earned Master’s degrees in both Mathematics and Computer Science. My supervisors were Anne Driemel and Stefan Hougardy. In my Master’s thesis, I analyzed the fine-grained complexity of a similarity measure between curves that is resistant to outliers. This work led me to pursue a Ph.D., where I explored classical problems such as clustering, nearest neighbor identification, and curve segmentation.
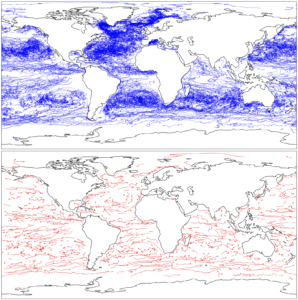
Throughout my Ph.D. studies, we have developed various tools to approximate complex problems involving polygonal curves and distance measures like the Fréchet Distance and Dynamic Time Warping. A highlight is our research on Subtrajectory Clustering, which identifies frequent patterns in large spatio-temporal datasets. This work has applications in climate science, robotics, and medicine. Our algorithms achieve near-optimal theoretical running times and strong empirical performance. I am particularly proud of our contribution to coresets for Dynamic Time Warping, proving that accurate approximations are possible even in non-metric curve spaces.
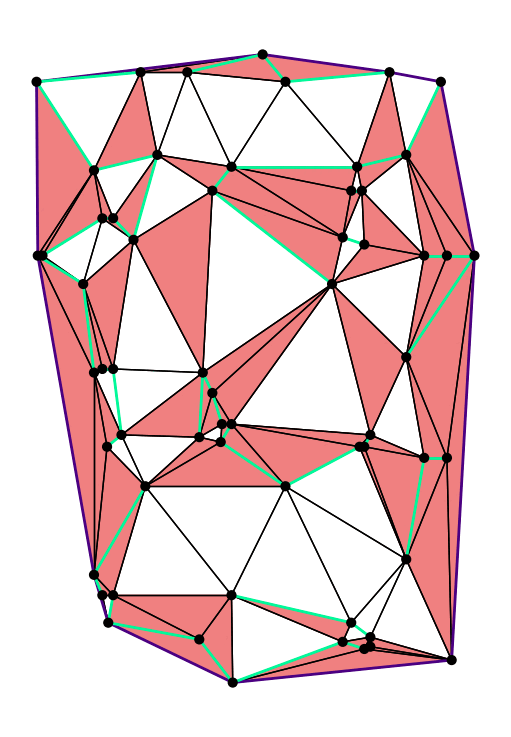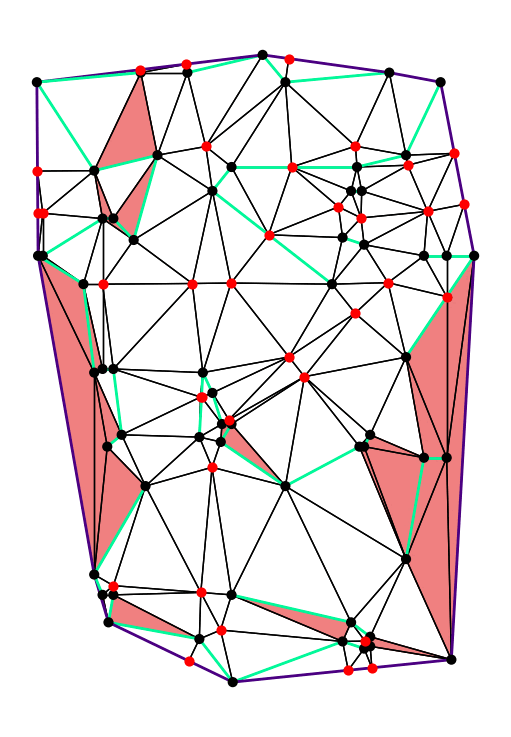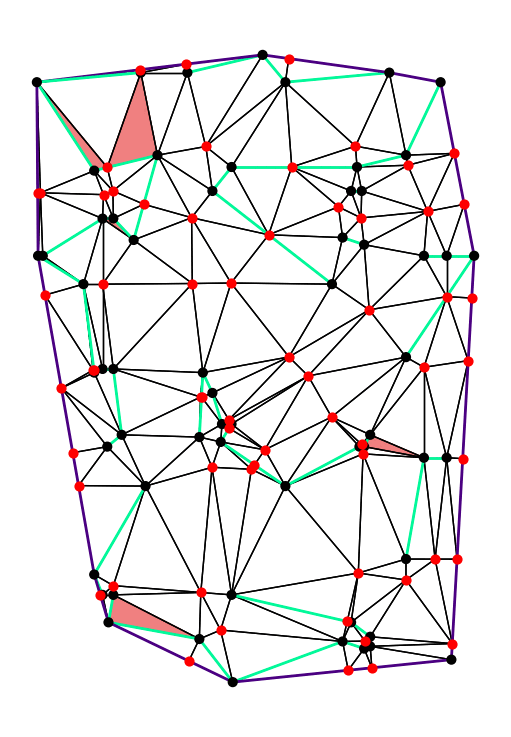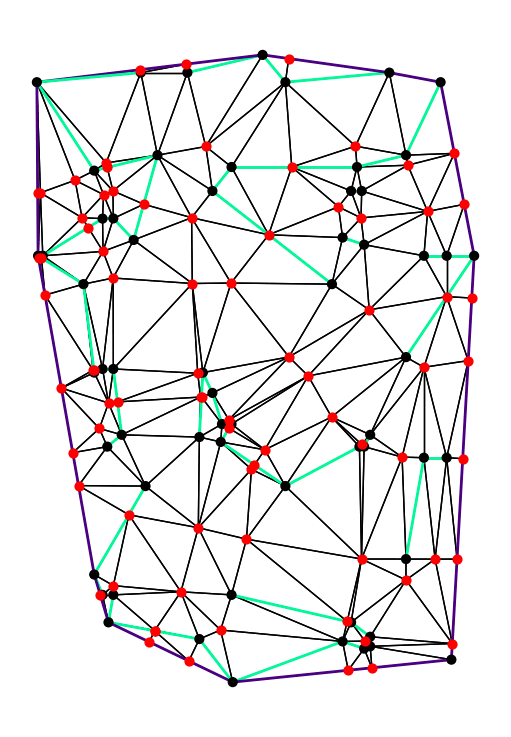More recently, I have worked on polygon triangulations that enable efficient and accurate finite element analysis. My team won the CG:SHOP 2025 challenge, and we presented our results at CG Week 2025 in Japan. Other problems I have worked on recently include a well-behaved variant of the classical Art Gallery Problem, as well as more general forms of shape matching for polygons.
I am passionate about teaching and sharing the beauty—and difficulty—of mathematics and computer science. My teaching experience includes courses in robotics, artificial intelligence, computational topology, and computational geometry, delivered in both English and German.
Beyond research, music has been a constant in my life. I have played the cello for nearly 20 years and actively participated in the Collegium Musicum Bonn and the Studentisches Blasorchester Bonn. I served as a member of the steering committee of the Collegium Musicum Bonn. When not immersed in academic work, I stay busy with triathlon training, programming contests, cooking, and video games.